Банки, сервисы подписок, магазины предлагают нам хорошие скидки, беспроцентные кредиты и прочие прелести. Только плати. Давайте разберемся, как можно оценить выгодность предложений с точки зрения инвестора.
Скидки-скидки-скидки
Покажу на своем примере.
У меня заканчивался оплачиваемый срок хостинга моего блога. Зашел на сайт к провайдеру для продления услуг. Посмотрел способы оплаты тарифа и задумался. Предлагалось продлить тариф оптом - с определенной скидкой:
- при оплате за год - скидка 12%;
- при оплате за два года - 24%;
- за три года - 36%.
Как понять какая скидка оптимальная? На первый взгляд все они дают примерно одну и ту же выгоду - экономию 12% за каждый год. Но тогда, при увеличении оплачиваемого периода - скидка будет стремиться к 100%, а размер оплаты к нулю.
К примеру, при оплате сразу за 8 лет - скидка должна быть 96%. А это точно нереально.
Поэтому пришлось обратиться к математике. Вернее к электронным таблицам (Google / Excel).
Для расчета выгодности я использовал функцию RATE (или Ставка). Она в основном используется для расчета процентной ставки по кредитам. Но для наших целей тоже подойдет.
Исходные условия:
- Если платить помесячно, за год набегает 100 рублей (взял круглое число для удобства).
- При оплате сразу за год - 88 рублей (скидка 12%).
- При оплате за 2 года - 76 рублей в год (скидка 24%).
- Оплата за 3 года - 64 руб/год (скидка 36%).
Какое из предложений самое выгодное?
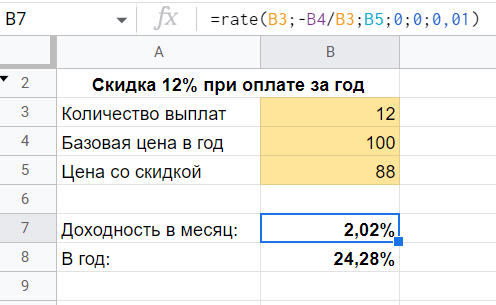
Посчитаю сначала выгодность 12% скидки.
Формула следующая:
=RATE(12;(-100/12); 88; 0; 0; 0,01)
где
- 12 - количество периодов (месяцев);
- 100/12 - платеж в месяц (сколько бы я платил без скидки 100 рублей в год или по 8,33 рубля в месяц);
- 88 - текущая стоимость услуги (с 12% скидкой).
Считаем:
Получаем, что 12% скидка на годовую услугу дает мне выгоду 2% в месяц или 24,3% в год.
Как это трактовать?
Представим есть только 88 рублей. У меня два варианта оплатить подписку на год.
- Я могу сразу оплатить годовую услугу с 12% скидкой. Отдам свои 88 рублей.
- Или же могу ежемесячно вносить платежи по 8,33 рубля (без скидки). Но моих имеющихся 88 рублей хватит на оплату всего 9 полных месяцев. Где взять остальное? Нужно разместить деньги под проценты и ежемесячно выдергивать часть на оплату услуги. Чтобы имеющихся денег хватило на оплату годовых услуг требуется доходность на вложенный капитал не ниже 24,3% годовых.
Если я не могу разместить свои деньги с гарантированной доходностью +24,3% годовых, то вариант с помесячной оплатой для меня будет не выгоден.
12% скидка на оплату годовых услуг эквивалентна доходности в 24% годовых!
Для других вариантов у меня получилось следующее:
- при оплате за два года я получаю выгоду 2,32% в месяц или 27,9% в год;
- при оплате за три года - выгода 2,64% или 31,7% в год.
Получается, что самым выгодным предложением является скидка в 36% при оплате за три года. Она на треть выгоднее, по сравнению с оплатой за один год.
Аналогичные расчеты выгодности можно сделать и для других сервисов подписок, которые предлагают вам различные скидки при оплате своих услуг. Ниже я дам ссылку на файл-шаблон с расчетами. Вам нужно только подставить свои данные.
Согласитесь, довольно неожиданно было увидеть выгоду в 24% годовых от скидки всего в 12%. Наш мозг не привык к таким кульбитам. Этим кстати пользуются многие банки, предлагая различные кредитные программы. Вернее пользовались. Сейчас по закону банки обязаны озвучивать процентную ставку по кредиту.
Но лазейка обмануть клиента осталась. Ведь у нас есть беспроцентный кредит или рассрочка.
Считаем выгодность рассрочки
Рассмотрим обратный пример на примере программ рассрочек.
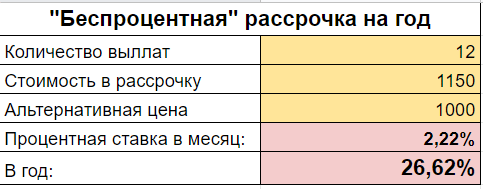
Нам предлагают смартфон в беспроцентную рассрочку по цене 1 150 каких-то денег. Рассрочка на год с ежемесячными выплатами равными частями.
В другом магазине подобный гаджет можно купить за 1 000. Естественно деньги сразу.
Вопрос: во сколько процентов годовых нам обойдется беспроцентная рассрочка?
Результат расчетов:
Простыми словами, покупка телефона в беспроцентную рассрочку эквивалентно кредиту со ставкой 26,6% годовых.
Результат еще можно ухудшить. Обычно при покупке товаров мы используем карты с кэшбэком. При рассрочках такого нет.
Что если у нас есть карта, дающая 5% кэшбэк на покупку. Как сильно от этого изменится результат?
Считаем:
У клиента всегда есть выбор: купить товар за свои и с кэшбэком или взять "беспроцентную" рассрочку под 36,8% годовых.
Готовый шаблон с формулами
По ссылке, шаблон с готовыми формулами и расчетами. Лежит в гугл-таблицах. В таблице меняйте только желтые ячейки. Чтобы утащить себе, нужно сделать копию файла.
- Меню "Файл - > Создать Копию" - для Гугл.
- Чтобы сохранить в Excel - "Меню - > Скачать"









Спасибо за статью!
Отлично расписано, теперь есть материал по которому можно обучить окружение 🙂
Отличная статья!
Неожиданный взгляд на обыденную вещь.
В первом примере не мешало бы учесть инфляцию. Во втором — выгоду от размещения денег на накопительном счете на протяжении периода рассрочки. Результат противоположным вряд ли бы стал, но ощутимо изменился бы
Совершенно верно. Автор это необоснованно упустил и результат может измениться как раз ощутимо, особенно при текущем росте цен на тарифы в сфере услуг.
Обожаю ваш сайт. Хоть и не следую в слепую. Хранить и приумножать доход. Вы мой первый учитель. Гуру так сказать. Удачи мой любимый сайт.
Красивый подход использовать RATE в этом случае.
Поделюсь своей находкой.
Задача такая:
Есть текущий капитал К, есть некая ставка доходности сверх инфляции С , которую я имею наглость снимать с капитала до самой смерти. Есть предполагаемая дата смерти (М месяцев до смерти).
Вопрос: сколько денег я могу изымать ежемесячно (в текущих ценах), чтобы к моменту смерти мой депо был равен 0. Т.е. какую пенсию я могу начать платить себе прямо сейчас.
В целом задача решается так: пенсия равна аннуитетному платёжу по кредиту размером К, ставкой С и продолжительностью М месяцев. Только в данном случае я кредит не беру, а даю (отдал капитал «бирже» в кредит, и снимаю ежемесячно аннуитет в виде пенсии). Функция Excel =-ПЛТ(С;М;К), ставку нужно правильно из годовой привести к месячной (См=(1+Сг)^(1/12)-1)).
Аналогичным способом решается обратная задача. Допустим я хочу пожизненную пенсию П, какой мне нужен размер капитала? =-ПС(С;М;Пенсия)
И пара мыслей на тему С и М.
Очевидно, чтобы всё это работало, нужную доходность (сверх инфляции!) нужно будет обеспечивать и сейчас и в 80 лет, страдая маразмом. Поэтому в оценке доходности надо быть весьма консервативным. Хороший ориентир даёт ОФЗ-ин — в целом они гарантируют 2,5%-НДФЛ сверх инфляции.
По поводу М — это очень важный параметр. Он сильно влияет на результат.
С одной стороны конечно хочется жить 100 лет. Но с другой стороны если планировать траты до 100 лет, то пенсия будет маленькая.
Если же М сильно занизить, то есть шанс, что наступит 70, ты ещё не умер, а денег уже 0.
Пришлось долго думать на этот счёт. В итоге после сверки с данными статистики лично для себя я остановился на возрасте 80 лет.
При этом как дополнительная подстраховка исхожу из того, что 1) скорее всего с определённого возраста траты начнут уменьшаться. (Имею ввиду, что да, на лекарства наверное тратить стану больше, но многие развлечения (и самое дорогое из них — путешествия) скорее всего будут становится не по здоровью). 2) сложно сказать, что будет лет через 20, но всё таки какую-то минимальную гос пенсию полюбас будут платить, что опять же даст возможность растянуть выплаты в случае, если окажусь долгожителем.
В общем сии размышления (о сроке жизни, ставке, желаемой пенсии) оказались весьма полезны для стратегического планирования.
Excel-ка со всеми формулами есть, могу прислать.
Выкладывайте сюда, кому интересно заберут
https://docs.google.com/spreadsheets/d/1Z7y0105ptsWKwD2cgH43dwVeigetAc3c-HsqXB30QtM/edit?usp=sharing
Мой любимый автор! Всегда удивляюсь его взгляду и расчетам практически на все! Респект! Учи, учусь, буду учиться!
Спасибо!
Какая неожиданная тема статьи! Спасибо автору, никогда не задумывалась о таких вещах.
А как, например, быть, когда известна беспроцентная рассрочка (колич-во платежей и сумма каждого), но не понятно, сколько бы стоила корзина товара без рассрочки? Где выгода? Сейчас раскручивается популярность сервиса «долями». Сама им пользуюсь, на первый взгляд переплаты там нет